Advent of Code

But this time, the maze is dynamic. Sort of. We start with an empty 71 by 71 grid (or 7 by 7 in the sample example), and we have a list of coordinates. These coordinates will be blocked in order. So using the first few coordinates in the example:

Part 1 - day 16, basically

In the first part this dynamic aspect doesn’t really apply, although it was pretty clear that it was going to come up in part 2. Here we have to apply the first 1024 steps, then find the length of the shortest path from top left to bottom right. So it’s mostly about reusing and slightly adapting the code from Day 16.

The main difference is that we no longer care about tracking directions, as there is no longer a cost associated to turning. I still decided to use my Node class, but now the neighbours are just a list of positions rather than pairs of Direction, Node:

Position = namedtuple("Position", ["row", "column"])

class Node:
    def __init__(self, position: Position):
        self.position: Position = position
        self.neighbours: list[Position] = []
        self.is_start: bool = False
        self.is_end: bool = False

    def add_neighbour(self, neighbour: Position):
        self.neighbours.append(neighbour)

    def remove_neighbour(self, neighbour: Position):
        if neighbour in self.neighbours:
            self.neighbours.remove(neighbour)
    
    def get_neighbours(self) -> list[Position]:
        return self.neighbours
    
    def __repr__(self):
        return f"Node({self.position})"
    
    def __str__(self):
        if self.is_start:
            return 'S'
        if self.is_end:
            return 'E'
        return '.'

    def __eq__(self, other):
        if type(other) == Position:
            return self.position == other
        elif type(other) == type(self):
            return self.position == other.position
        raise TypeError(f"Cannot compare {type(self)} with {type(other)}")

The reason I used Position rather than Node for the neighbours was initially so that it was easier to test if a neighbour is already in the list. This is because by default, two Nodes will only count as “equal” if they are the exact same instance of the object. So:

a = Node(Position(1, 1))
b = Node(Position(1, 1))
assert a == b

Will be False. Unless you specify a __eq__(self, other) method to specify how two objects can be compared, which I eventually had to do anyway to make things easier in part 2. But I didn’t want to change the neighbours again, so I left it as is. In my __eq__, implementation, we can compare either to a Position or to another Node, and they will register as equal if the positions are the same.

We now initialize the grid as just an empty grid, with all neighbours connected. It’s the same code as in Day 16, except we no longer read the data from the file, we just go through all possible coordinates.

def init_empty_grid(width: int, height: int) -> tuple[dict[Position, Node],
                                                      Node,
                                                      Node]:
    nodes = {}
    for r in range(height):
        for c in range(width):
            n = Node(Position(r, c))
            nodes[Position(r, c)] = n
            if (ln := nodes.get(Position(r, c-1))) is not None:
                n.add_neighbour(ln.position)
                ln.add_neighbour(n.position)
            if (tn := nodes.get(Position(r-1, c))) is not None:
                n.add_neighbour(tn.position)
                tn.add_neighbour(n.position)

    sn = nodes[Position(0, 0)]
    en = nodes[Position(height-1, width-1)]
    sn.is_start = True
    en.is_end = True
    return nodes, sn, en

We can easily parse the input into a list of nodes, first splitting by line break, then by ,. The coordinates in the file are X, Y (horizontal then vertical), which is the opposite convention from ours, so we have to be careful to switch the order.

def parse_input() -> list[Node]:
    data = []
    with open("day18", 'r') as fp:
        data = fp.readlines()
    data = [[int(v) for v in d.split(',')] for d in data]

    return [Node(Position(r, c)) for c, r in data]

Since I guessed there would be a dynamic aspect to part 2, I directly implemented a way to dynamically get “the next n blocks” from the list, and to alter the maze. To do that, we have to get all the neighbours of the node to block, remove the node from their neighbours list, and then delete the node from the map.

def next_block(data: list[Node], blocksize: int):
    if len(data) == 0:
        return [], []
    block = data[:blocksize]
    remainder = data[blocksize:]
    return block, remainder


def block_nodes(mapnodes: dict[Position, Node], blocknodes: list[Node]):
    for node in blocknodes:
        if node.position not in mapnodes:
            continue
        # remove from neighbours
        for n in mapnodes[node.position].get_neighbours():
            mapnodes[n].remove_neighbour(node.position)
        # remove node
        del mapnodes[node.position]

And as in Day 16, all that is left is to solve the maze. We reuse the same method, except that we remove all the things related to the direction checks, and we only return a single best path. I’ve also already put here the only addition from Part 2, which is the UnsolvableMazeException, which is raised is there is no valid solution to the maze.

def insert_sorted(l: list[tuple[int, Any]], v: tuple[int, Any]) -> list[tuple[int, Any]]:
    for i, (c, _) in enumerate(l):
        if v[0] < c:
            l.insert(i, v)
            return l
    l.append(v)
    return l

class UnsolvableMazeException(Exception):
    pass

def solve_maze(start: Node, grid: dict[Position, Node]) -> tuple[int, list[Node]]:
    paths: list[tuple[int, list[Node]]] = []
    
    for n in start.neighbours:
        insert_sorted(paths, (1, [grid[n]]))

    # keep track of best score at visited -> if we revisit something which already has a 
    # better score -> stop that path!
    visited: dict[Position, int] = {}

    while len(paths) > 0:
        cur_cost, cur_path = paths.pop(0)
        cur_node = cur_path[-1]
        for n in cur_node.get_neighbours():
            if n not in cur_path:
                new_cost = cur_cost+1
                if n in visited and visited[n] <= new_cost:
                    # abandon this path
                    continue
                visited[n] = new_cost if n not in visited else min(new_cost, visited[n])
                path = (new_cost, cur_path + [grid[n]])
                paths = insert_sorted(paths, path)
                if grid[n].is_end:
                    return path
    
    raise UnsolvableMazeException()

data = parse_input()
block, data = next_block(data, blocksize)
nodes, start, end = init_empty_grid(w, h)
block_nodes(nodes, block)

best_path = solve_maze(start, nodes)
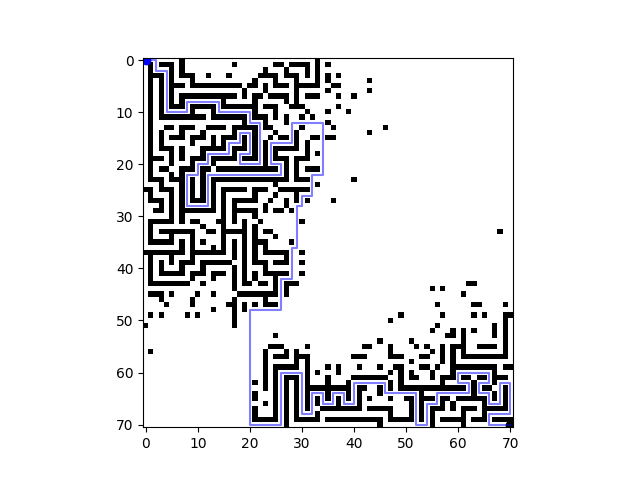
print(f"Part 1 answer: {best_path[0]}")

Part 2 - blocking blocks

Here is where the dynamic aspect quicks in. At some point as the blocks keep adding up… there will be no possible path between the start and end points. We have to find out which block is the blocking block.

This was relatively easy based on my implementation of part 1. Since we have the best path returned by our maze solver, and we already have a way to get the next block, all we have to do is:

while len(data) > 0:
    block, data = next_block(data, 1)
    block_nodes(nodes, block)
    # Only update the best path if it is now blocked 
    if block[0] in best_path[1]:
        try:
            best_path = solve_maze(start, nodes)
        except UnsolvableMazeException:
            print(f"Unsolvable maze after adding node {repr(block[-1])}")
            return

Quick update

So I’ve just seen a better solution for part 2, which is to use a Binary search method: we now that the block we are looking for is somewhere between block 1024 and the end of the list. So we try in the middle: is the path blocked? If yes, our first blocking block is between 1024 and that middle value, otherwise it’s between that middle value and the end of the list. Iterating like that would reduce the number of maze-solving steps.

But I checked and, in my code, thanks to the “skip if the new block wasn’t in the path” check, I only need to solve the maze 54 times (and I skip it 1874 times), so I’m comfortable just keeping my solution, especially since it’s not dependent on knowing when the list ends (we could have an infinite stock of blocks in an ever-expanding grid, and it would still probably work).