Advent of Code

Day 13 was an easy one for me, a welcome relief from the past few days. The setup of the puzzle is that we have a bunch of machines with two buttons. Pushing on a button moves a claw by a certain amount in the X and Y axis. For each machine, there is a prize located at a certain X, Y position. The input is a list of machine descriptions, as in the example:

You always start at \((0, 0)\). So for instance, in the first machine, if you push A 80 times, you get to position \((80 \times 94, 80 \times 34) = (7520, 2720)\). Then, if you push B 40 times, you get to position \((7520 + 40 \times 22, 2720 + 40 \times 67) = (8400, 5400)\), which is the position of the prize. Great!

Part 1: eyes on the prize

Pushing buttons, it turns out, has a cost: 3 tokens for button A, 1 token for button B. The puzzle is: what is the minimum amount of tokens that you have to spend to get all the prizes that are possible to get.

The first step in solving the puzzle is recognizing that the whole thing about “minimum amount of tokens”, and of different costs per button, is a red herring, a useless piece of information. Each machine defines a system of two equations with two unknowns (the number of button pushs for A and B), and there are really three possible outcomes for each machine:

Let’s write this system of equations. Let \(X_A, Y_A\) be the movement in \(X\) and \(Y\) that you get from pushing button A (and \(X_B, Y_B\) the same for button B). Let \(X_P, Y_P\) be the coordinates of the prize, and \(A\) and \(B\) the amount of pushes for each button, with \(A, B \in \mathbb{N}^+\). We have:

\(A\) and \(B\) are our two unknowns. There are several ways of solving the system. I went with a matrix representation:

\[\begin{pmatrix} X_P \\ Y_P \end{pmatrix} = \begin{pmatrix} X_A && X_B \\ Y_A && Y_B \end{pmatrix} \begin{pmatrix} A \\ B \end{pmatrix}\]

This can be interpreted as a transformation of \(A, B\) coordinates into \(X, Y\) coordinates. What we are looking for is the inverse transform. From the equation above, we isolate \(\begin{pmatrix} A \\ B \end{pmatrix}\):

\[\begin{pmatrix} X_A && X_B \\ Y_A && Y_B \end{pmatrix}^{-1} \begin{pmatrix} X_P \\ Y_P \end{pmatrix} = \begin{pmatrix} A \\ B \end{pmatrix}\]

So we just need to invert a \(2 \times 2\) matrix, which is a fairly easy process. Given a matrix \(\begin{pmatrix} a && b \\ c && d \end{pmatrix}\), the inverse is \(\frac{1}{ad-bc}\begin{pmatrix} d && -b \\ -c && a \end{pmatrix}\). If \(ad-bc\) (the determinant) is \(0\), then there is no solution.

Is this a programming puzzle or a math exam?

While I was solving the system of equation and translating all of this into code – which I promise I’ll get to – I was thinking about THE TWIST. I was convinced that something would happen that made this nice 2 by 2 matrix inversion become a lot more complex. Just adding one more equation to the system (by adding a button and a vertical dimesion, for instance) would be annoying to recode. Or adding a nonlinearity somehow.

I almost didn’t go the matrix inversion route and code a more brute-force version. The puzzle instructions mentioned that “each button would need to be pressed no more than 100 times”, which made searching the space of all possible solutions very easy… but that looked suspiciously like a trap as well. So I eventually just coded the matrix inversion solution. But first…

RegEx time, again.

We need to parse the input. We can load it as a string, and first split by double line break \n\n to get the instructions per machine. Then we split by line, and make a regex to parse the button parts and another regex to parse the prize location part, leaving us with the integers that we need for the rest:

Vector = namedtuple("Vector", ["X", "Y"])

def parse_button(s: str) -> Vector:
    x, y = re.findall(r'X\+(\d+), Y\+(\d+)', s)[0]
    return Vector(int(x), int(y))

def parse_prize(s: str) -> Vector:
    x, y = re.findall(r"X=(\d+), Y=(\d+)", s)[0]
    return Vector(int(x)+add_to, int(y)+add_to)

def parse_input():
    with open("day13", 'r') as fp:
        data = fp.read()
    # split first by machine
    machines = data.split('\n\n')
    inputs = []
    for m in machines:
        a_state, b_state, prize_state = m.split('\n')
        inputs.append((parse_button(a_state), parse_button(b_state), parse_prize(prize_state)))
    return inputs

Now we solve the equation for each machine. First we check if the determinant is equal to zero. If not, we invert the matrix, and check if we have integer solutions.

def solve(xy_a, xy_b, xy_v) -> tuple[int, int]:
    """Solve: 
        a*x_a + b*x_b = x_v
        a*y_a + b*y_b = y_v
        
        (x_a x_b  (a  = (x_v 
         y_a y_b)  b)    y_v)

        (a b)^T = D^-1 (x_v y_v)^T
         """
    
    D = [[xy_a.X, xy_b.X],[xy_a.Y, xy_b.Y]]
    det = D[0][0]*D[1][1] - D[0][1]*D[1][0]
    if det == 0:
        return 0, 0
    
    adj = [[D[1][1], -D[0][1]], [-D[1][0], D[0][0]]]
    a = (adj[0][0]*xy_v.X + adj[0][1]*xy_v.Y)/det
    b = (adj[1][0]*xy_v.X + adj[1][1]*xy_v.Y)/det

    if a==round(a) and b==round(b):
        return int(a), int(b)
    
    return 0, 0

inputs = parse_input()
total = 0
for xy_a, xy_b, xy_v in inputs:
    ans = solve(xy_a, xy_b, xy_v)
    total += ans[0]*3 + ans[1]

print(f"Part 1 answer: {total}")

Part 2: go big or go home

In part 2, we increase the location of the prizes by 10000000000000, a.k.a. a lot.

This would be very annoying if I was brute-forcing the solution, but it doesn’t change anything in our case.

inputs = parse_input("")
offset = 10000000000000
total = 0
for xy_a, xy_b, xy_v in inputs:
    xy_v = Vector(xy_v.X+offset, xy_v.Y+offset)
    a, b = solve(xy_a, xy_b, xy_v)
    total += a*3 + b

print(f"Part 2 answer: {total}")

Not so fast

I actually did fail the second part initially. Because I was paranoid that floating point rounding errors would make the a == round(a) check fail, I initially used math.isclose(a, round(a)) instead. What I hadn’t really notice is that, by default, isclose uses a relative tolerance of 1e-9, which when the numbers are as high as what we have here mean that non-integer answers could easily pass the test. I could have put an absolute tolerance instead, but I tested the simpler == and saw that it actually worked fine here.

Bonus: all solutions

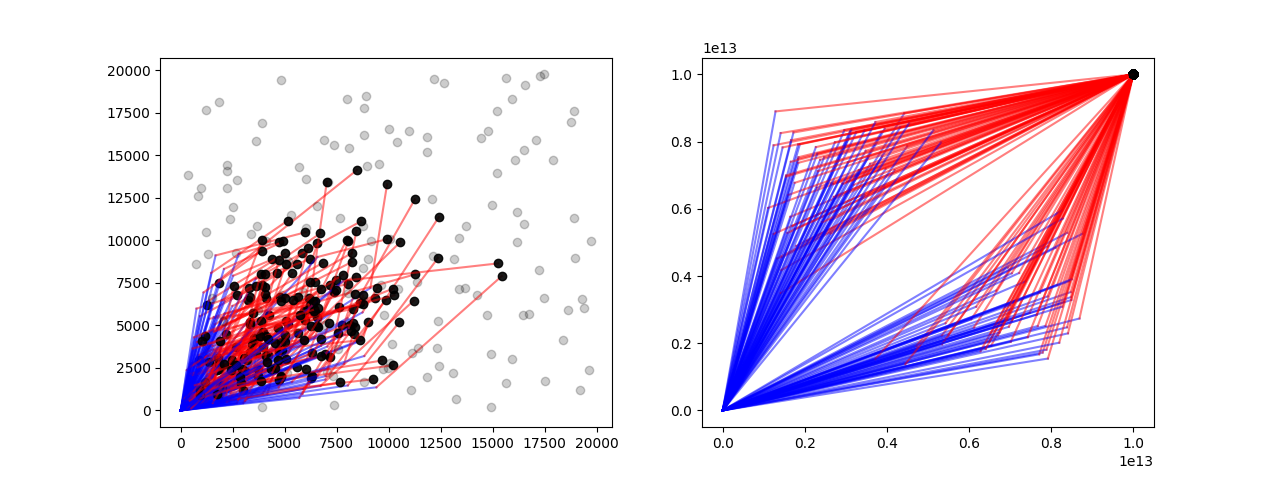
Here is a plot of all solutions for part 1 and 2, with blue lines representing the result of pressing the A button, and red lines the results of pressing the B button. Greyed dots are prizes which are unreachable by their machine.